群馬大学 | 医学部 | サイトトップ | Software Tips | RについてのTips
最終更新: 2008年 9月 5日 (金曜日) 12時41分 :2群の平均値の差の検定について加筆修正
統計処理の王道というか,普通に段階を踏んで統計処理をするには,統計処理の羅針盤に書いたような手順で進めればいいのだが,たくさんの変数を処理するには,ある程度定型的な処理を簡単な関数の形でまとめてしまった方が,実用上便利である(もちろん邪道だが)。ここではそのような関数のまとめ方を例示する。
なお,せっかく余計な出力が出ないように加工するのだから,プログラムをバッチ実行する際など,まとめ関数を実行する前に,sink("result.txt")などとして結果の出力先ファイルを指定しておき,終了後にsink()として出力先をコンソールに戻せば,実行プログラム自体が含まれないファイルが得られる(プログラム実行過程自体はもちろんログに残るが)。
まず,ヒストグラムを作ったりシャピロ=ウィルクの検定によって分布の正規性をみて,正規分布にあてはまっていると思われない(けれども2群の分布の形は似ている)ならWilcoxonの順位和検定を行い,そうでなければ平均値の差の検定(常にWelchの方法による)を行う(注:念のために書いておくと,正規分布と有意差があるからといって(この場合,第2種の過誤をみていることになるので,有意水準は0.2にすることが多い),常に機械的にノンパラにすればいいということはないし,逆に,正規性が棄却されなくてもノンパラにした方がいい場合もある。検定手法の選択には,データ以前にその変数について得られている知識,例えば先行研究からの知見を考慮すべきである。また,その専門分野の慣習も考慮するのが無難である。ただし,Wilcoxonの順位和検定をしているのに,結果の統計量として中央値と四分位偏差を示さずに平均値と標準偏差を示すような整合性のなさは避けるべきだと思う)。図示は層別箱ヒゲ図か,平均値と標準偏差によるエラーバーを重ね書きしたストリップチャートが良いと思われる。
平均値の差の検定をする場合,かつては下に関数定義したように,分散の差をみて,有意差がなければ等分散を仮定したt検定,そうでなければWelchの検定をするという2段階の検定をするべきというのが多くの統計の教科書の説明であったが,最近では常にWelchの検定をするのがよいことがわかっているので,この関数定義は既にobsoleteであり,歴史的意味とRのコーディングテクニック例という以上の意味をもたない。常にWelchにするなら関数定義はもっとシンプルになる。
auto.location.test <- function(X,B,TITLE=NULL,ALPHA=0.05,BETA=0.2) {
# XかBのどちらかが欠損ならばTRUEになる論理ベクトル.MISSINGを定義
.MISSING <- is.na(X)|is.na(B)
# [!.MISSING]をつけることでXもBも欠損でない要素だけを抽出し,実数型として.Xに付値
# Rではas.singleはas.doubleと同義で,倍精度実数(のベクトル)を意味する
.X <- as.single(X[!.MISSING])
# .Xの変数名属性にXに渡された実引数の変数名属性を付値
names(.X) <- paste(deparse(substitute(X)))
# [!.MISSING]をつけることでXもBも欠損でない要素だけを抽出し,カテゴリ変数として.Bに付値
.B <- as.factor(B[!.MISSING])
names(.B) <- paste(deparse(substitute(B)))
# .Bのカテゴリ数(水準数)は,度数分布表の長さを求めることで得られる
.NUMCATS <- length(table(.B))
# 2群が成立しなければエラーメッセージを表示して処理を止める
if (.NUMCATS!=2) { cat("カテゴリ数が2ではないので検定できません。\n"); return(FALSE) }
# TITLE引数が省略されたら長さ0なので仮の表題を作り,そうでなければTITLE引数をそのまま
# 表題として.TITLEという変数に付値。
if (length(TITLE)<1) { .TITLE <- paste("位置母数の比較:",deparse(substitute(X)),"by",deparse(substitute(B))) } else { .TITLE <- TITLE }
# 表題を出力
cat(.TITLE,"\n")
# .Xについてシャピロ=ウィルクの正規性の検定を行い,結果をnormalityという変数に付値
normality <- shapiro.test(.X)
# 正規性の検定の結果の有意確率がnormality$p.valueに得られるので,それが第2種の過誤より
# 小さければ正規分布に従うという帰無仮説が棄却されると判断し,normaldistという論理変数
# にFALSE(偽)を与える。そうでなければTRUE(真)を与える。
if (normality$p.value < BETA) {normaldist <- FALSE} else {normaldist <- TRUE}
# 正規性の検定の結果を表示
cat("分布の正規性: W=",normality$statistic,"\t p=",normality$p.value,"\n")
# 正規分布していれば,
if (normaldist) {
# 等分散性の検定を実行
equalvariance <- var.test(.X~.B)
# 等分散という帰無仮説が棄却されたらWelchの方法でt検定し,そうでなければ
# var.equal=Tという引数をつけてt検定して,結果をequalmeanに付値
if (equalvariance$p.value < BETA) { equalmean <- t.test(.X~.B) } else {equalmean <- t.test(.X~.B,var.equal=T) }
# 2群のサンプルサイズ,平均値,不偏標準偏差を計算
.N.X <- tapply(.X,.B,length)
.MEAN.X <- tapply(.X,.B,mean)
.SD.X <- tapply(.X,.B,sd)
# 2群それぞれについて表示
for (.J in 1:.NUMCATS) {
.CATNAME <- names(table(.B))[.J]
cat(.CATNAME,":\t N=",.N.X[.J],"\t 平均値=",.MEAN.X[.J],"\t 不偏標準偏差=",.SD.X[.J],"\n")
}
# 層別ストリップチャート表示
stripchart(.X ~ .B, method="jitter", vertical=T, main=.TITLE)
# 平均値と不偏標準偏差のバーを書き込むための横軸上の位置を示すベクトル定義
# 層別ストリップチャートの中心位置が1と2にあるので,それよりやや右に表示するため
# 0.15を加える
.I.X <- 0.15 + 1:2
# 層別ストリップチャートに2群の平均値を追記
points(.I.X,.MEAN.X,pch=18)
# 不偏標準偏差のバーを下から上に向かって追記
arrows(.I.X,.MEAN.X-.SD.X,.I.X,.MEAN.X+.SD.X,code=3,angle=90,length=.1)
# 検定結果を最小限に絞って表示
cat("等分散性の検定: F=",equalvariance$statistic,"\t p=",equalvariance$p.value,"\n")
cat("平均値の差の検定: t=",equalmean$statistic,"\t df=",equalmean$parameter,"\t p=",equalmean$p.value,"\n")
}
# 正規分布でなければ
else {
# Wilcoxonの順位和検定を実行
equalmedian <- wilcox.test(.X~.B)
# 2群それぞれについてサンプルサイズ,中央値,四分位範囲(Q1-Q3という形で表示)を計算
for (.J in 1:.NUMCATS) {
.CATNAME <- names(table(.B))[.J]
.N.X <- length(.X[.B==.CATNAME])
.FV.X <- fivenum(.X[.B==.CATNAME])
.MEDIAN.X <- .FV.X[3]
.IQR.X <- paste("[",.FV.X[2],"-",.FV.X[4],"]")
cat(.CATNAME,":\t N=",.N.X,"\t 中央値=",.MEDIAN.X,"\t 四分位範囲=",.IQR.X,"\n")
}
# 層別箱ヒゲ図を表示
boxplot(.X~.B,main=.TITLE)
# 検定結果を最小限に絞って表示
cat("Wilcoxonの順位和検定: W=",equalmedian$statistic,"p=",equalmedian$p.value,"\n")
}
}
この関数を使って検定をしてみるには,まずこの関数を読み込ませてから(インターネットに接続された環境ならRのプロンプトに対して,
と打てばよいはず),例えば,
QUANTITY <- c(runif(100),runif(100)+0.1) BINARY <- c(rep(1,100),rep(2,100)) auto.location.test(QUANTITY,BINARY)
とすると,大抵の場合(乱数によっては偶然正規分布から外れない場合がありえるので例外もある),下図のような箱ヒゲ図が描かれるとともに,その下のような検定結果が表示される。
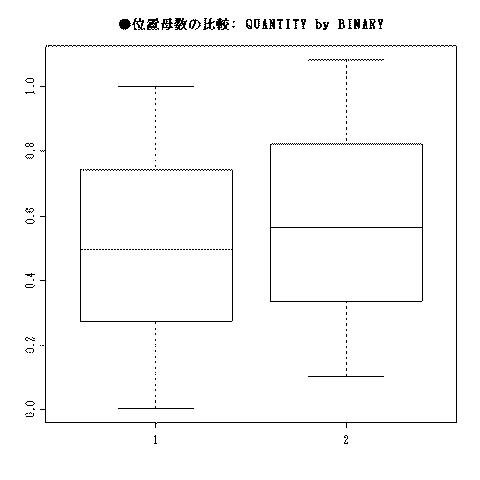
●位置母数の比較: QUANTITY by BINARY 分布の正規性: W= 0.9605487 p= 2.268620e-05 1: N= 100 中央値= 0.4977598 四分位範囲= [ 0.273357099038549 - 0.741803372395225 ] 2: N= 100 中央値= 0.564918 四分位範囲= [ 0.335410046996549 - 0.821300017554313 ] Wilcoxonの順位和検定: W= 4177 p= 0.04446429
また,正規乱数2群の比較をしてみると,例えば,
QUANTITY <- c(rnorm(100),rnorm(100)+0.1) BINARY <- c(rep(1,100),rep(2,100)) auto.location.test(QUANTITY,BINARY,TITLE="2群の正規乱数100個ずつの母平均の差の検定")
とすると,大抵の場合(これも乱数によっては例外となる場合もあるかもしれない),下図のようなストリップチャートが描かれるとともに,その下のような検定結果が表示される。
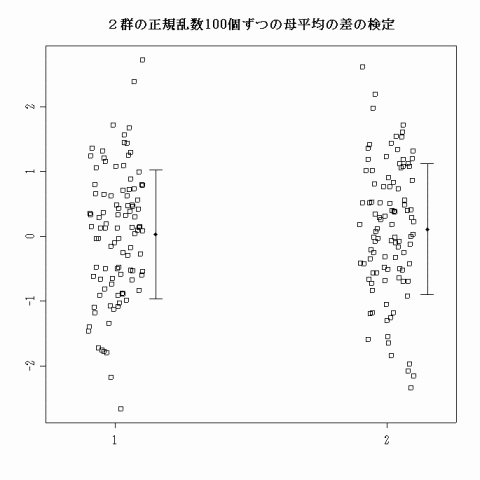
2群の正規乱数100個ずつの母平均の差の検定 分布の正規性: W= 0.99517 p= 0.7745815 1: N= 100 平均値= 0.03128780 不偏標準偏差= 0.9934966 2: N= 100 平均値= 0.1105606 不偏標準偏差= 1.010095 等分散性の検定: F= 0.9674049 p= 0.869384 平均値の差の検定: t= -0.5595192 df= 198 p= 0.5764398
2つのカテゴリ変数のクロス集計表を作り,各々のカテゴリが2つ以上あればFisherの直接確率で検定する。まとめ関数定義は以下の通り。
autocrosstable <- function(A,B,TITLE=NULL) {
if (length(TITLE)<1) { .TITLE <- paste("クロス集計:",deparse(substitute(A)),"×",deparse(substitute(B))) } else { .TITLE <- TITLE }
cat(.TITLE,"\n")
missing <- is.na(A)|is.na(B)
.A <- as.factor(A[!missing])
.NAME.A <- paste(deparse(substitute(A)))
.B <- as.factor(B[!missing])
.NAME.B <- paste(deparse(substitute(B)))
.FOK <- (length(table(.A))>=2)&(length(table(.B))>=2)
.TAB <- table(.A,.B)
names(dimnames(.TAB))<-c(.NAME.A,.NAME.B)
.SUMA <- table(.A)
.SUMB <- table(.B)
.ALL <- sum(.TAB)
.PTAB <- rbind(cbind(.TAB,.SUMA),c(.SUMB,.ALL))
rownames(.PTAB) <- c(names(.SUMA),"SUM")
colnames(.PTAB) <- c(names(.SUMB),"SUM")
print(.PTAB)
if (.FOK) {
r.fisher <- fisher.test(.TAB)
cat("Fisherの正確な確率検定: p=",r.fisher$p.value,"\n\n")
} else {
cat("カテゴリ数が1以下の変数があるので検定不可\n\n")
}
mosaicplot(.TAB,main=.TITLE)
}
200個ずつの一様乱数を発生させ,等間隔にカテゴリ化することによって2水準のカテゴリ変数と4水準のカテゴリ変数を作り,クロス集計してみるのは,以下のプログラムでできる。cut()は量的な変数を,任意の値で区分してカテゴリ化する関数である。
XR <- runif(200) YR <- runif(200) X <- cut(XR,br=c(0,0.5,1)) Y <- cut(YR,br=c(0,0.25,0.5,0.75,1)) autocrosstable(X,Y)
実行すると,下図のようなモザイクプロットが描かれ,その下にあるようなクロス集計表と,Fisherの正確な確率検定の結果が得られる。
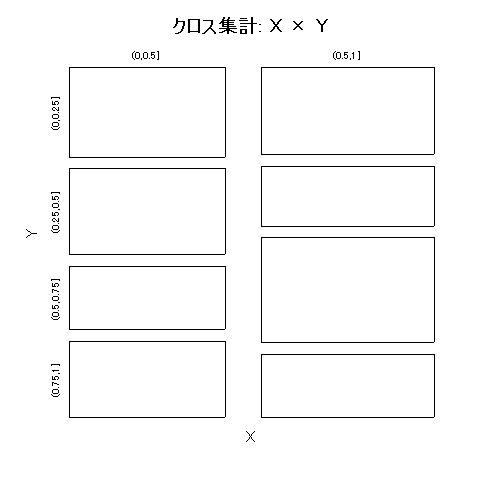
クロス集計: X × Y
(0,0.25] (0.25,0.5] (0.5,0.75] (0.75,1] SUM
(0,0.5] 27 26 19 23 95
(0.5,1] 29 20 35 21 105
SUM 56 46 54 44 200
Fisherの正確な確率検定: p= 0.155802
独立変数Xのばらつきで従属変数Yのばらつきをどのようにどれくらい説明できるかを調べるため,回帰分析をすると同時に散布図を描き,回帰直線を重ね書きし,回帰直線の95%信頼区間と95%予測区間(従属変数の予測値の95%信頼区間)を重ね書きする。統計量の出力も加工したいところだが,現状ではそこは手をつけずにsummary()のままにしてある。まとめ関数定義は以下の通り。
linear.reg <- function(X,Y) {
# 欠損値対策
.MISSING <- is.na(X)|is.na(Y)
.X <- as.numeric(X[!.MISSING])
.NAME.X <- paste(deparse(substitute(X)))
.Y <- as.numeric(Y[!.MISSING])
.NAME.Y <- paste(deparse(substitute(Y)))
.res <- lm(.Y ~ .X)
print(summary(.res))
# matplot()とかmatlines()を使う方が簡単だが,敢えて1本ずつ描く
plot(.Y ~ .X, type="p", xlab=.NAME.X, ylab=.NAME.Y, pch=20)
abline(.res, lty=1)
# ここで変数.Xをもつデータフレームを横軸のために定義する
.XX <- data.frame(.X=seq(range(.X)[1],range(.X)[2],length=20))
.plim <- predict(.res, .XX, interval="prediction")
.clim <- predict(.res, .XX, interval="confidence")
lines(.XX$.X, .plim[,2], lty=2)
lines(.XX$.X, .plim[,3], lty=2)
lines(.XX$.X, .clim[,2], lty=3)
lines(.XX$.X, .clim[,3], lty=3)
mtext(paste(.NAME.Y,"=",coef(.res)[[1]],"+",coef(.res)[[2]],"*",.NAME.X))
}
たぶん半分くらいは独立変数によって説明されるような例を考えるため,サイズ100の(0,1)の一様乱数ベクトルXXXを作ってから,それに(0,1)の一様乱数を加えてYYYを作り,独立変数XXX,従属変数YYYとするのは下記の通り。
XXX <- runif(100) YYY <- runif(100) + XXX linear.reg(XXX,YYY)
以下のような(乱数によって変わってくるが)グラフと回帰分析結果の出力が得られる。
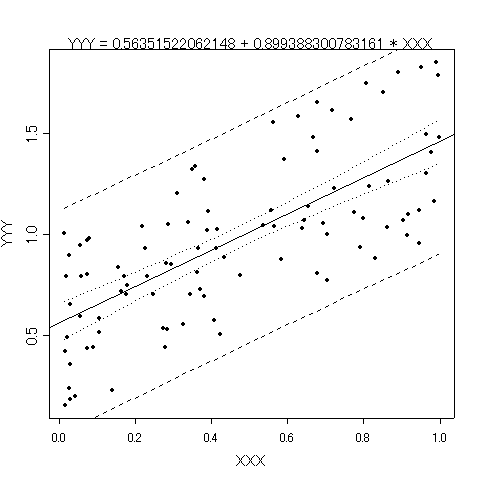
Call:
lm(formula = .Y ~ .X)
Residuals:
Min 1Q Median 3Q Max
-0.46224 -0.20665 -0.01268 0.23322 0.48857
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.56352 0.04869 11.57 <2e-16 ***
.X 0.89939 0.08681 10.36 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.2758 on 98 degrees of freedom
Multiple R-Squared: 0.5227, Adjusted R-squared: 0.5179
F-statistic: 107.3 on 1 and 98 DF, p-value: < 2.2e-16
Correspondence to: minato@phi.med.gunma-u.ac.jp.