リーマン・ゼータ関数まわりのこと
■川端裕人『算数宇宙の冒険 アリスメトリック!』実業之日本社,ISBN 978-4-408-53563-0(Amazon | bk1)を読み,解説を書かれている柏野雄太さんのサポートページを見て触発されたので,Rでリーマン・ゼータ関数まわりのことがどれくらいできるのか試してみた。
■とりあえずゼータ関数を探してみたら,VGAMライブラリ[manual pdf]とgslライブラリ[日本語版マニュアル……このgslというライブラリはGNU Scientific LibraryをRに実装したもののようだ]に入っていた。どちらも関数名はzeta()であった。
■しかし,VGAMでもgslでもリーマン・ゼータ関数は整数あるいは実数に対してしか定義されていないので,解析接続(注:この概念が今一つ良く理解できていないのがいけないんだけれども)ができず,柏野さんのページで示されているような図は作れない。Rでも複素数(complex)の四則演算などはできるのだが(例えば,x <- 1+1iと打ってから,x*2と打てば[1] 2+2iと表示されるし,x^2と打てば[1] 0+2iと表示される),zeta()は複素数を引数にとれず,gslでは虚部が捨てられて計算されてしまうし,VGAMではNAになってしまうのだった。
■実数範囲でできることは,例えばζ(2)=π2/6[式1]を確かめてみるとか,ζ(2),ζ(3),...,ζ(n)とnを増やしていったときの挙動を図示してみるといったことである。これは,Rで普通に試せる。
■最初の例は,ζ(2)=1+1/(2^2)+1/(3^2)+...という無限級数だから,とりあえず一万項くらいやってみるには,
sum(1/(1:10000)^2)
とすればいい。出力結果は,[1] 1.644834となる。一方,円周率はpiとして組み込まれているので,[式1]の右辺は,
pi^2/6
でいい。出力結果は,[1] 1.644934となる。つまり,ちょうど一万分の一の誤差があるわけである。誤差が見えなくなるまで項数を1桁ずつ増やしていったら,千万項が必要なことがわかった。つまり,
sum(1/(1:10000000)^2)
の結果は,[1] 1.644934となった。なお,後で青木先生からご指摘を受けた通り,コンピュータでの数値計算の常識として,小さい方から足さないと計算誤差が出るので,足し算は小さい方からやるべきと考えたら,
sum(1/(10000000:1)^2)
と書く方がいい。けれども,実はRではどちらでも小さい方から計算されているようだ。つまり,明示的に繰り返しループを書くと,
a <- 0; for (i in 10000000:1) a <- a+1/i^2; a
とした方がいいということだ。この場合はoptions(digits=20)くらいにしないと違いがわからないのだけれども,確かに
a <- 0; for (i in 1:10000000) a <- a+1/i^2; a
とすると,結果に微妙な誤差が出る。
■(2009年12月11日追記)黒川信重編著『数学セミナー増刊:リーマン予想がわかる』日本評論社の巻頭,桜井進「高校生からわかる――超入門:リーマン予想」に書かれていた,オイラーが求めた収束が速い関数というのは,本当に収束が速かった。つまり,
sum(1/((1:50)^2*2^(0:49)))+log(2)^2
の出力結果は,options(digits=20)のとき[1] 1.644934066848226となって,完璧にpi^2/6と一致した。
approxzetatwo <- function(x) { sum(1/((1:x)^2*2^(1:x-1)))+log(2)^2 }と関数定義してから,sapply(1:50,approxzetatwo)とすると,実は41項目で同じ結果が得られていることがわかる。
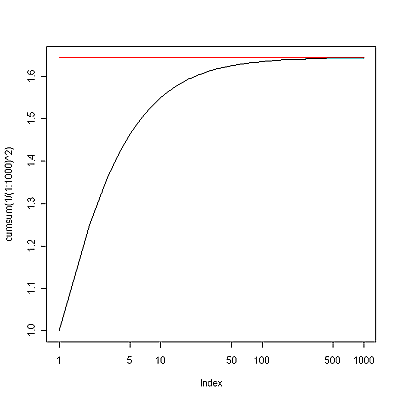
■計算する項数を増やすにつれて級数がpi^2/6という極限に近付いていく様子を図示するには,例えば,
plot(cumsum(1/(1:1000)^2),type="l",log="x") lines(c(1,1000),c(pi^2/6,pi^2/6),col="red")
とすれば下図が描ける。ここでは,見やすくするため項数を対数軸表示にした。なお,pi^2/6は,library(gsl)の後でなら,zeta(2)と置き換え可能である。参考までに書いておくと,ここまでの内容は,いつの間にかMaximaと融合し,Gnuplotも内蔵した高機能なものになったEulerというソフトでも,同じような感じで実行できる。
■続いて,ゼータ関数の引数を2以上の整数で徐々に大きくしていくとどうなるかを試してみる。もちろん,賢いgslライブラリを使えばplot(2:1000,zeta(2:1000),type="l",log="x")などということも簡単にできるが,定義式通りにx乗分の1を計算させてzeta()並みの精度を出すために一千万項まで計算させてしまうと,ζ(100)まででもハングアップしたかと思うくらいの途方もない時間がかかるのでやめておく方が無難である。
■そこで,計算させる項数を1万項くらいにとどめてζ(2)からζ(100)までの近似をプロットさせるには,べき乗関数powを定義してから,sapplyの結果の行方向の和をとればいいので,Rのコードは次の通りである。
pow<-function(x,y) x^y
plot(2:100,rowSums(sapply(1:10000,pow,-(2:100))),type="l",log="x",xlab="ζ(n)の引数n",ylab="ζ(n)")
require(gsl)
lines(2:100,zeta(2:100),col="red",lty=2)
legend("topright",lty=c(1,2),col=c("black","red"),c("近似","ζ"))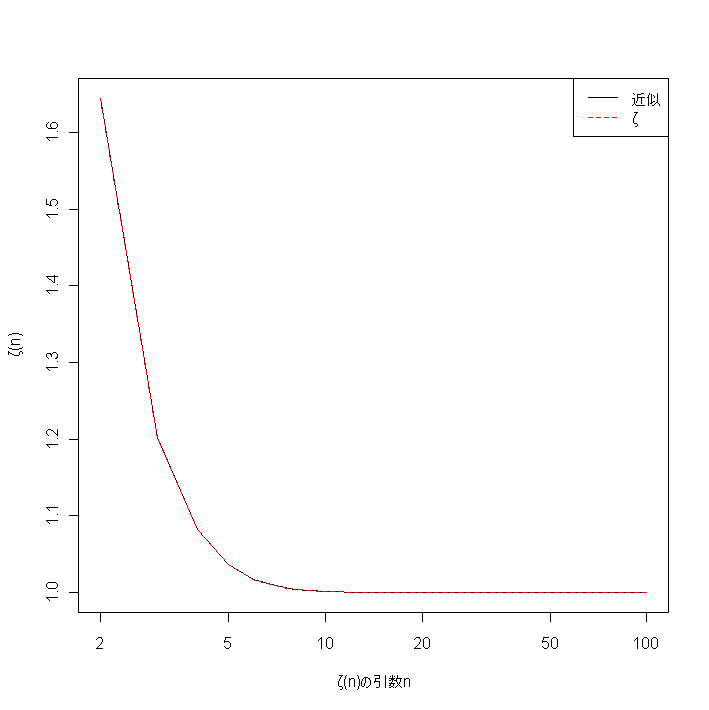
■上図のように横軸に2から100まで,縦軸にそれに対応するゼータ関数の近似値をとったグラフが描けるわけである。この状態でlines(2:100,zeta(2:100),col="red",lty=2)とすると,gslライブラリのゼータ関数で計算した値が重ね描きされる。パソコン画面くらいの解像度では,2つのグラフのズレはほとんどわからないくらいである。
■さていよいよ,複素数を引数にとれるゼータ関数だが,webを検索していたら,Javaで書かれたものが見つかった。コンパイル済みのもの(*.jar)しか公開されていないようだが,このソフトのソースを何とか入手してC++に移植すればRから呼べるかもしれない。しかし公開されていないわけだから,たぶんそれは難しいだろう。それで,このページに書かれていた式をそのままRに置き換えてZeta(s)を関数定義したら(但しもちろん無限和はできないので柏野さんに倣って500項の和にして),複素数を受け付けるゼータ関数ができた。もっとも,Zeta(-1)が-0.0833313となってしまうし(本当は-1/12だから-0.08333333となるはずだし,不思議なことにgslライブラリのzeta(-1)はそうなる。なぜ不思議かといえば,ζ(-1)=-1/12は解析接続をしたことで得られる解だからである),Zeta(2)は1.644930074848となってしまうので近似精度は低い。しかも,Rのガンマ関数gamma()が複素数を引数にとれないので実部が負の場合はまだ計算できない。
それでも,実部が正の場合,例えばZeta(1/2+1i)は計算できて, 0.144659-0.6974934iとなる。もし,これが正しければ,柏野さんのサポートサイトに載っていたグラフが作れるはずである。
複素ガンマ関数は,わざわざ作らなくても,gslライブラリにlngamma_complex()という対数をとった形で入っていることがわかった。exp()は複素数を通すので,これで複素数を通すζ関数の近似ができるはずである。また,大浦さんという方が開発されたライブラリにはCとFortranで複素ガンマ関数のコードが提供されているので,これをRに移植すればgslライブラリを使う必要がなくなるように思う。ぱっと見た感じではわかりやすいソースコードなので,そう苦労しなくても移植できそうな気がした。
■大浦さんのコードをRに移植し,複素数を受け付けるゼータ関数を改良してみた。500項の和だったところを1万項の和にしたら,Zeta(2)は1.644934となってくれたのだが,Zeta(-1)は実部は-0.0833333となってくれるものの,なぜか虚部がついてしまう。もう少し検討が必要か。
試しにgslライブラリを使って,Zeta()の関数定義中の複素変数のガンマ関数をexp(lngamma_complex(t))とした関数Zeta2()を定義したら,Zeta2(-1)は[1] -0.08333333+0iとなったので,移植したコードで虚部がついてしまったのは,計算精度の問題だったようだ。
■柏野さんのサイトで言及していただいたのにできていないのは悔しいので,とりあえずgslのlngamma_complex(t)を使ったZeta2()で図示してみる。
source("http://minato.sip21c.org/swtips/Zeta.R")
AbsZeta <- function(x) Mod(Zeta2(1/2+x*1i))
curve(AbsZeta(x),0,50)
lines(c(0,50),c(0,0))とすると,条件判定のところで警告メッセージが出る部分があるが,下図ができる。残念ながら計算精度が低いのか,非自明なゼロ点がきちんとゼロになってくれないのだが,だいたい近い形のグラフにはなる。
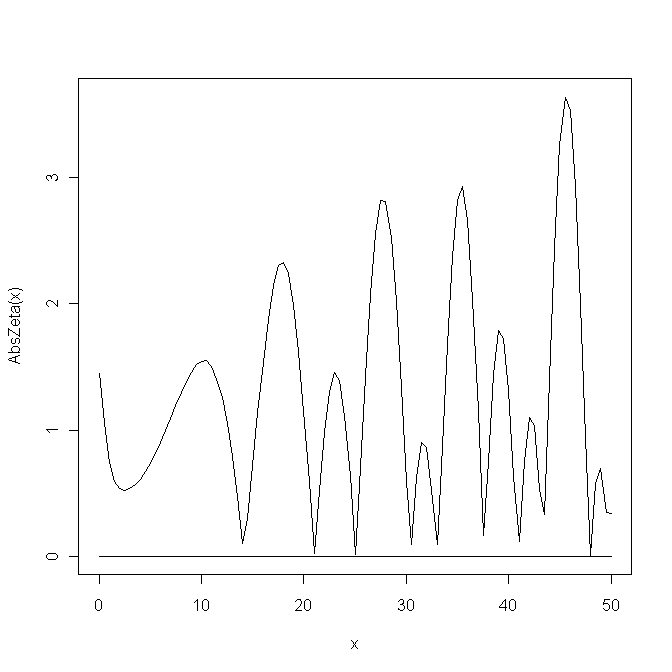
■(2010年5月19日追記)大きな勘違いをしていたのだが,上記欠点は,計算精度が低いというよりも,curve()だとステップが粗いため,非自明なゼロ点を与えるxが計算されていないということが原因だった。また,条件判定の警告は,Zeta2()関数がベクトル化されていないためであった。一方,Zeta2()を定義する部分は,100000項でなくて10000項でもZeta2(-1)が[1] -0.08333333+0iとなってくれたし,1000項でも[1] -0.08333328+0iとなった。以上を踏まえ,以下のように書き換えたコード(Zeta2.R)を試してみた。
require(gsl)
Zeta2 <- function(s) {
if (s==1) { ret <- Inf } else if (Re(s)>0) {
a <- 1/1^s
for (i in 1000:2) { a <- a + ((-1)^(i-1))/(i^s) }
ret <- 1/(1-2^(1-s))*a
} else {
t <- 1-s
ret <- 2*(2*pi)^(-t)*cos(t*pi/2)*exp(lngamma_complex(t))*Zeta2(t)
}
ret
}
AbsZeta <- function(x) Mod(Zeta2(1/2+x*1i))
x <- 0:50000/1000
y <- sapply(x,AbsZeta)
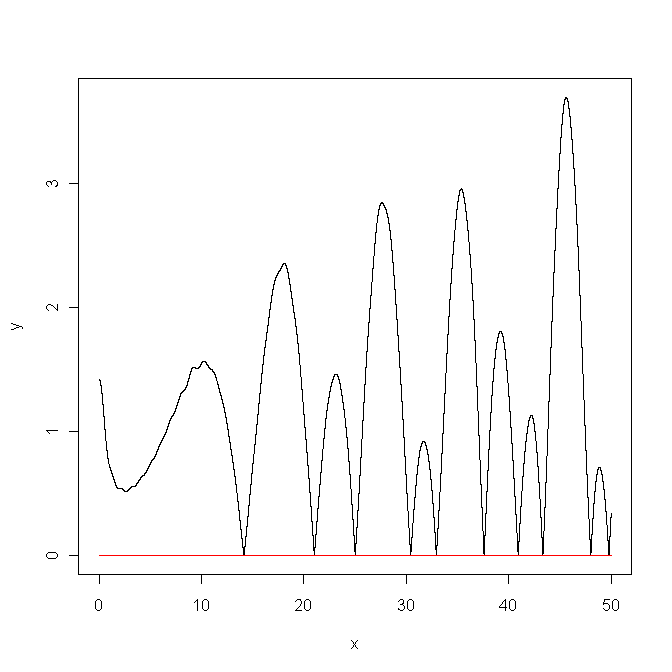
plot(x,y,type="l")
lines(c(0,50),c(0,0),col="red")かなりの計算時間がかかったが,下図の通り,ある程度満足のいくグラフになったように思う。速いコンピュータがあれば,Zeta2()の計算の項数を増やしたりAbsZeta()を描画するステップを細かくすれば,もっときれいなグラフが描けるだろう。
多倍長演算(2014年6月1日)
■滅多に使わないため,自分でもよく忘れるので,このページのアーカイヴからここにコピペしておく。
■(多倍長演算)Rで多倍長演算をサポートするパッケージは,gmpが便利である。gmpパッケージをロードすると,as.bigz()で多倍長整数,as.bigq()で多倍長実数を扱える(過去のメモ参照)。しかし,高精度計算と表示には,Rmpfr(R Multiple Precision Floating-Point Reliable)というパッケージの方が向いている。πなどの定数も高精度で含まれているからだ(pi,gamma,catalan,log2については,Const("pi",100)などとすれば高精度で得られる)。mpfr()という関数で高精度オブジェクトができ,そのまま計算ができる。なお,Const("pi",100)の結果はasin(mpfr(1,100))*2と一致するが,mpfr(pi,100)とは一致しないことには注意が必要である。mpfrになった値に関数を適用すると自動的に高精度計算になるが,逆では単なる型変換になってしまうので下位の桁は適当に補われるだけになる。100桁のexp(1)が欲しい時は,mpfr(exp(1),100)ではなくて,exp(mpfr(1,100))でなくてはいけない。
多倍長演算の表示について(2019年6月19日)
■このページの2014年9月22~23日のアーカイヴ(更新情報の保管庫4)から以下採録する。
■裏RjpWikiの「多倍長精度計算結果を見やすく出力」と,その元になった,r-statistics-fanの日記の「Rで多倍長精度計算~とりあえず10000の階乗を計算してみる」には明記されていないが,もちろん10000の階乗を計算するだけなら,library(gmp); factorial(as.bigz(10000))とするのが簡単。たぶん,整数の多倍長演算にはRmpfrパッケージよりgmpパッケージの方が向いていると思う。sink("factorial10000.txt")のようにしてから実行すれば,指定した名前のテキストファイルに結果を書き出せる。その後で出力をコンソールに戻すにはsink()とすれば良い。10桁ごとにスペースを入れて100桁ごとに改行させたければ次のようにすると思う。
library(gmp)
longfact <- function(x, n=100, m=10) {
z <- factorial(as.bigz(x))
siz <- ceiling(log10(z))
p <- n - (siz %% n)
res <- paste(rep("_", p), sep="", collapse="")
res <- paste(res, as.character(z), sep="", collapse="")
q <- (siz + p)/m
for (i in 1:q) {
cat(substr(res, (i*m)-m+1, (i*m)))
cat(ifelse((i %% m)==0, " \n", " "))
}
}
longfact(10000)
■「r-statistics-fanの日記」のスコットランド独立賛成票が素数~Rで素数をチェックする関数色々を拝読し,library(gmp); n[sapply(sapply(n, factorize), length)==1] とか?とtweetしておいたら,記事に追記してくださった。gmpパッケージの高性能さは感動的。
■鵯記にguestさんからいただいたコメントの通り,gmpパッケージにおけるfactorial(as.bigz(10000))は,たぶん実際にはfactorialZ(10000)を実行している。Rの思想としては型を指定し総称関数に渡すのが普遍的と思うので,ぼくは今後も最初の書き方をすると思うが。
フィボナッチ数列の計算と再帰処理について(2019年6月19日)
■上記多倍長演算のことをなぜ思い出したかというと,twitterでフィボナッチ数列の実数計算を使った一般項表示結果の丸め誤差の話が出てきた関連である。
元ネタはtogettterにまとめられているが,ExcelとLibreOffice Calcで挙動が違うという話だった。以下自分のtweetを採録しておく(このtweetから連投)。
△浮動小数点演算の丸め誤差が出ない方が特殊な処理だと思う。Rで A <- 1:25; B <- (((1+sqrt(5))/2)^A-(((1-sqrt(5))/2)^A))/sqrt(5); C <- numeric(25); C[1] <- C[2] <- 1; for (i in 3:25) { C[i] <- C[i-2] + C[i-1] }; B==C とやると4項目からFALSE
△確かにoptions(digits=20); Bとやると,4項目が3.0000000000000004となっている。25項目は誤差が5e-11を初めて超える項。ちなみにLibreOffice Calc 6.2.4.2 (x64)では,小数点以下16桁表示で10桁目に1が出るがB=CはTRUEを返す。
(たぶんExcelが何か特殊な処理をしている,と書いたら,奥村さんが過去にExcelの浮動小数点処理について検証した結果を教えてくださった)
△高精度計算をすれば一致するのかと思って,library(Rmpfr)してからone<-mpfr(1,1000); two<-mpfr(2,1000); rootfive<-sqrt(mpfr(5,1000)); AA< -mpfr(1:25,1000); (((one+rootfive)/two)^AA-(((one-rootfive)/two)^AA))/rootfive としても1,2,3,4,6項目しか整数にならないしCと一致しない。1000ビット精度だが。
△ちなみに最後を BB <- (((one+rootfive)/two)^AA-(((one-rootfive)/two)^AA))/rootfive としてから、sprintf("%20.15f", BB)とすれば小数点以下15桁までは0という精度で計算できていることが確認できる。仮に10000ビット精度で計算しても定義通りに足し算したCの値とは一致しない。
☆参考までに,関数化したコードを載せておく。fib0がフィボナッチ数列の定義通りの演算。fib1が再帰呼び出し版,fib2が末尾再帰の再帰呼び出し版(ただしfib2(1000)などとするとスタックが深すぎるというエラーが出るので,本来の意味での末尾再帰にはなっていないようだ。これら再帰呼び出しについてはかつての記述を採録した下記参照),fib3が通常の計算による一般項,fib4がRmpfrパッケージを使った高精度計算版である。
■フィボナッチ数列といえば,以前末尾再帰をRで書くコードを考えた時に触れたので,ついでにその記事(2014年3月24日,更新情報の保管庫3)も採録しておく。
■Rで書かれたアッカーマン関数のコードを見て,
Rは素直な再帰でも1行で,
ack <- function(m, n) { ifelse(m==0, n+1, ifelse(n==0, ack(m-1,1), ack(m-1, ack(m, n-1)))) }
とtweetした後で数値入力して調べたら,(3, 5)までは計算できたが,(3, 6)や(4, 1)はスタックが溢れて計算できないことがわかった。options(expressions=500000)としておくと,デフォルトのoptions(expressions=5000)では計算できないack(3, 6)は計算できるようになるが,それでもack(3, 7)やack(4, 1)は計算できない(ノードスタックが溢れる。ちなみに1行でifelse()を使う代わりに複数行でif () else ()という形で書くと,使うスタックが変わるようだ。いずれにせよ溢れるが)。柏野さんから,Haskellなどではスタックを食わない末尾再帰(tail recursion)が普通というご指摘があり,調べたところ,2012年時点ではRではサポートされていないとのこと。現状では,ループを使って非再帰で書くしかないようだ。エレガントでないが仕方が無い。
■RでAckermann関数を書く話の続き。あのシュールな巨大数寿司屋漫画の作者の方が作られたのであろうページに掲載されているC++版なら,Rに移植できそう。途轍もなく遅そうだけれど(なお,考えてみれば,ack(4, 1) = ack(3, ack(4, 0)) = ack(3, 13)なので,m=4のハードルの高さは自明だった)……と書いたら,柏野さんから,移植では無くRcppでそのまま使う方がいいのでは? というsuggestionをいただいた。確かにその通りかもしれない。Rで末尾再帰は絶対に無理かというと,このPythonコードのように,アルゴリズム自体を工夫して末尾再帰にしたものは,Rに移植できた。つまり,フィボナッチ数列を素直に再帰定義するコードは,
fib <- function(n) ifelse(n<=2, 1, Recall(n-1)+Recall(n-2))
となるが,これだとn=20程度でもスタックが深くなりすぎて計算不能になってしまうところ,
fib2 <- function(n, a1=1, a2=0) ifelse(n<=1, a1, Recall(n-1, a1+a2, a1))
と書けば,無駄な計算をしなくなりスタックが深くならないので大きなnでも高速に結果が出る(2019.6.21追記:fibとfib2の定義が0始まりになっていたので通常の1始まりに書き換えた)。奥が深い。ちなみに,関数定義内でRecall()と書くのと定義される関数名をそのまま書くのは同じことだが,Recall()だと別名にコピーして元のオブジェクトをrm()しても大丈夫だが,定義される関数名をそのまま書いてしまうと,同じ操作で使えなくなってしまうので,Recall()の使用がお勧めらしい。結局,3月24日に東に向かう新幹線の中で,前述のC++で書かれた非再帰版アッカーマン関数をRに移植してしまった。このコードは,ポインタを配列の添字にしたので,メモリ操作的には非常に無駄が多いが,移植自体はうまくできたと思う。ただ,これでack(4, 1)などやろうものなら,いったいどれくらいの時間が必要か見当も付かない。
Correspondence to: minato-nakazawa[at]umin.net.