【第686回】 講義準備など（2014年5月25日）
- 6:30に新大阪着。JRで三宮に行き，地下鉄で名谷へ。名谷PATIOのモスバーガーで朝食をとってから大学へ。
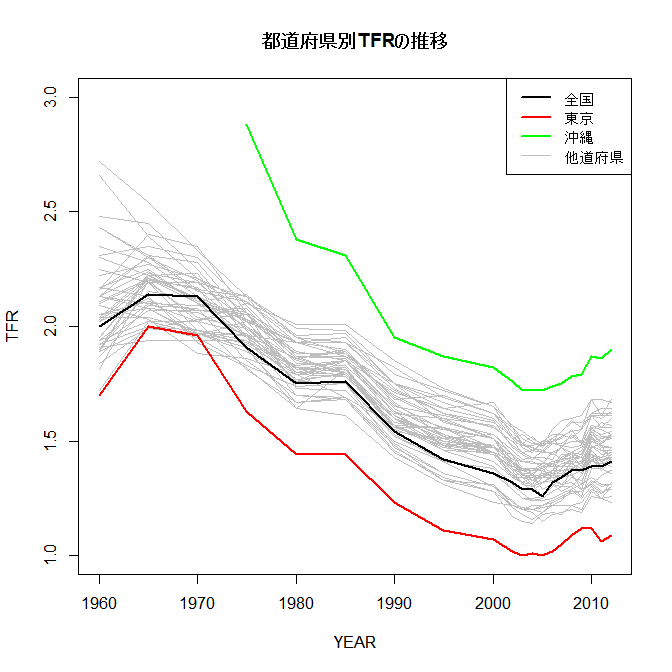
電車の中と食事中は，新大阪駅構内の本屋で見つけて買った，『ハードナッツ！』のノベライズ本（蒔田光治，山浦雅大，徳尾浩司[脚本]，豊田美加[ノベライズ]『ハードナッツ！ 数学girlの恋する事件簿』角川文庫，ISBN 978-4-04-101624-4（Amazon | honto | e-hon））を読んでいた。見逃していた第１回と第２回の部分を読んだら，感度や特異度が高くても有病割合が低いと陽性反応的中度が低くなるという話だと思っていた部分は，微妙に違っていた（大した違いではないが）。「精度」が99.9％と書かれていて，くるみと伴田刑事の会話では，「１万人に１人がかかる難病で，検査精度は10000人が受けに来たら，9990人が正しい判定ということ」とされていた。スクリーニングにおいて，検査陽性の人のうち本当に病気の人をa人，実は病気でない人をb人，検査陰性だけれども実は病気の人がc人，検査陰性の結果通りに病気でない人がd人とすると，感度はa/(a+c)，特異度はd/(b+d)，陽性反応的中度はa/(a+b)，陰性反応的中度はd/(c+d)なのだが，ハードナッツの言うところの「精度」は(a+d)/(a+b+c+d)であって，どれとも合わない。有病割合が1/10000という稀な疾病であることから，ここでのくるみの論理は「一万人が検査を受けたとすると（…中略…）10人には間違った判定が下る。ということは，本当に病気なのは一万人にひとりのはずなのに，病気と判定される人が10人くらい出てきてしまうってことなんです。だから，伴田さんの病気の確率は，99.9％じゃなくて，10人のうちのひとり，せいぜい10％ってことなんです」となっていて，結局は有病割合が低いから陽性反応的中度はせいぜい10％くらいだろうという話に帰着するのだけれども。もう少し丁寧に書くと，有病割合は(a+c)/(a+b+c+d)だから1万人が検査を受けたらa+c=1のはずで，伴田刑事の状況はスクリーニングで陽性判定が出た段階なのでa+bの中に含まれており，1から精度を引いた値を考えるとb+c=10だから（a+c=1を代入するとb=a+9となる），くるみが言いたいことは，a/(a+b)＝a/(2a+9)，かつこの関数はaが-9/2の点を除けば連続で単調増加なので（注：a/(2a+9)をaで微分すると(2a+9-2a)/(2a+9)^2＝9/(2a+9)^2なので常に正），a/(a+b)が取れる値は，0<=a<=1ではa=1のとき最大になり，1/11だ！ ということになる。「せいぜい」というのは「多く見積もっても」という意味であり，1/11を計算するとわずかに9％は超えているから，「せいぜい10％」という表現はまったく正しいのか。- 講義準備の前に，昨日も触れた東京のTFRが他道府県とはかけ離れて低いというグラフ（右上）を，e-Statからデータをダウンロードして自動的に描くRコードを書いてみた。
- 講義準備を進めているうちに11:00になったので，事務に行って確認したところ，今日の後援会総会については，専攻主任とキャンパスツアーの案内以外の人には決まった仕事はないらしいので，とりあえず研究室で待機しつつ，講義準備を進めることができる。
- 環境・食品・産業衛生学は，毎回のことだが，前回の講義のミニレポート用紙に書かれている質問への回答集を作るだけでかなりの時間をとられる。17:00までかかって，漸く完了。これから明日の資料を準備する。
- 『ハードナッツ！』は，6月11日にDVDとBlu-rayのboxが発売され，6月24日からはNHKの地上波でも放送されるとのこと。今度こそ第1話と第2話を録画しよう。
- アフリカ学会で関西に来たという北大の山内さんと三宮で晩飯。バスで帰宅後，講義準備の続き。
- バスの中で『ハードナッツ！』を読了。第7話にも１つ突っ込みどころがあって，スズムシの鳴き声は普通の携帯電話じゃ伝わらないんじゃなかろうかということ。しかし全体としては面白いからいいか。続編希望。
△Read/Write COMMENTS
▼前【685】（PTAなど（2014年5月24日） ） ▲次【687】（講義と講義と原書講読とミーティング（2014年5月26日） ） ●Top